living computation
Symmetric divergence
Uh oh, jargon alert.
And this time we even have an actual equation down there, yikes… but really really, it’s not that bad, it’s kind of cool, and it actually relates to stuff…
But ah, if mathoidness is just too eye-glazing, it should be safe to view anything with an ‘=’ in it as just bad abstract art, and the words should still carry us through…
To play along at home: See if you can recognize the wise old saying this one is about.
- Designing viable machinery is hard
- Making machines programmable defers behavioral decisions and reduces their cost
- Research in computer scienceIncluding parts of artificial intelligence and neural networks, automatic programming, genetic and evolutionary computation, adaptive systems and machine learning, decision trees, Bayes networks… asks how machines can improve their own behavior automatically.
Twenty years ago I was involvedMostly I did the hacking, the data collecting, and a lot of the writing. (And geek pride jargon alert: I contributed the term ‘bias’ to refer to the negative of a threshold…) in the development of a learning algorithm for a thing called a Boltzmann MachineWe capitalized ‘Machine’ — because both words were supposed to be part of the name — but it seems the field didn’t buy that for long, and now says ‘Boltzmann machine’ at least as often..
A Boltzmann Machine gets some input bits from its environment, and then it produces some corresponding output bits, depending on what’s inside the machine.
A key trait is that the Boltzmann Machine has randomness built into
it. Even given constant inputs, over time it will generate a variety
of sets of output bits, according to the probability
distributionFor example, with two input bits a and b,
and one output bit c, a conditional probability distribution
could be:
which amounts to a slightly randomized exclusive-or (‘either
or, but not both’) truth table from inputs to output. stored
within it.If input Probability that ab is c is
0 c is 1 00 0.95 0.05
01 0.05 0.95
10 0.05 0.95
11 0.95 0.05
We train a Boltzmann Machine by presenting it with samples drawn from some desired input-output probability distribution, and it changes its internal programming in an attempt to match the probability distribution it observes.
Over time the Boltzmann Machine learning algorithm tends to minimize a particular quantity called the asymmetric divergenceThe same quantity goes by many names, including Kullback-Leibler distance or Kullback-Leibler divergence, and relative entropy., often denoted by the letter G, measuring how well the machine’s internal probability distribution matches the desired distribution.
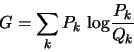
Breaking it down: k stands for a ‘state’ — which is any combination of input and output bit values — and we’re going to sum up (∑) over all possible statesEven though the equation doesn’t actually say anything about ‘all possible states’…we’re just supposed to know that, because it would clutter up the equation to include it. Really, equations are all about preaching to the converted, and sometimes they get so elliptical that they might as well be only abstract art.. Pk is the probability of state k occurring in the real world, as a fraction from 0 to 1, and Qk is how often that state occurs inside the machine.
First we divide the ‘correct’ probability Pk by
the machine’s estimated probability QkA Boltzmann
Machine must never think any state k is completely
impossible, since then Qk=0 and we could be facing
the dreaded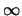 
.. Then
we have to deal with that ‘log’ thing; fortunately we mostly only need
to know there is that log(1)=0, so that if
Pk/Qk=1Meaning the machine’s
Q probability exactly matched the world’s P, for
that k., then that k contributes nothing to the value
of G.
If the machine gets the probabilities of all possible states exactly right, the overall value of G will be zeroIt turns out that no matter how bad a job the machine does, G can’t be negative, but it isn’t immediately obvious why that would be..
OK, we need an example: Assume just one input bit and one output
bit, so two bits total and therefore four possible states k
overall. Then given some P and Q values (that each have
to sum up to 1.0, because they are probabilities), we could compute
G like this:
| k | PkSome hypothetical ‘correct’ state probabilities, according to the world. | QkThe probabilities we imagine the machine is currently producing. | Pk/Qk | log(Pk/Qk) | Pk log(Pk/Qk) | Running G |
| 00 | 0.10 | 0.23 | 0.435 | -0.362The log of a number greater than zero but less than 1 is always negative | -0.0362 | -0.0362Note how the running value of G is actually negative here. It’ll be positive by the time we’re done. |
| 01 | 0.40 | 0.28 | 1.429 | 0.155 | 0.062 | 0.026See? Positive already. Why? Because P is on top in the fraction, and also out front multiplying the log. So those cases when Pk is bigger than Pk (producing a positive log) tend to be heavily weighted, while the ‘negative log’ cases (as when k=00 above) tend to be discounted. |
| 10 | 0.40 | 0.41 | 0.976 | -0.011 | -0.0043 | 0.0215 |
| 11 | 0.10 | 0.08 | 1.25 | 0.097 | 0.0097 | 0.0312 |
| Final G | 0.0312 | |||||
If you exchange the roles of P and Q in the computation of G you generally get a different answerIn the table above, for example, computing G with P and Q swapped gives 0.0365, rather than the 0.0312 ‘distance’ from Q to P., which is why it is called the asymmetric divergence.
The asymmetry arises because G weights each of the ‘log error terms’ using the Pk’s, so an error associated with a large Pk probability gets a lot of weight, while k’s with small Pk’s are more or less irrelevant.
Like one’s morning routine, perhaps, frequent events can tend to become highly optimized, while a gross inability to shower efficiently in zero gravity, say, is unlikely to matter.
It all makes sense, it does, it does…
So, the asymmetric divergence is rightly asymmetric; because learning is all about moving the machine’s image of reality to match better the actuality.
And learning does seem so essential, to the success of our species…
It all makes sense…but the urge to complete the symmetry, somehow, is overwhelming.
It would have to be about some backwards G’ measure:
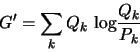
In bizarro G’ land, the important cases would be the ones that occur frequently inside the machine, regardless of how often they happen in the real world.
And minimizing G’ is about changing the world to make it more like what’s in your mind. About making your dreams come true.
Yes.
Call it D, say, the symmetric divergence:
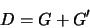
It seems D really captures the depths: When there is a mismatch between reality and the mind of the machine, there is a choice, always a choice. The machine can try to learn to match reality, or the machine can try to change reality to match its mind. Maybe a shower in zero gravity would be fun.
G or G’? Wisdom.
